Approche probabiliste du prix de la construction et gestion de l’aléa prix
« L’aléatoire n’est qu’un modèle, plus ou moins convenable, de notre ignorance de l’espace physique dans lequel nous vivons ».
Le prix total d’un lot (exemple : sol souple) est la somme de plusieurs prix. Chaque prix est le produit d’une quantité et d’un prix unitaire.
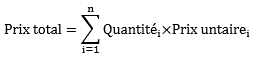
Chaque quantité est connue de manière probable, c’est-à-dire qu’il est possible que la quantité varie légèrement. Cela peut provenir de :
- Incertitude de précisions du métré ;
- Métré différent d’un métreur à l’autre (métré du sous-traitant différent de notre métré) ;
- Quantité réellement mise en œuvre différente de celle métrée…
Chaque prix unitaire est connu de manière probable, c’est-à-dire qu’il est possible que le prix unitaire varie légèrement. Cela peut provenir de :
- Calcul de moyenne sur plusieurs prix (bibliothèque de prix) ;
- Rabais appliqué de manière intuitive (prestation sous-traitée) ;
- Durée des négociations avec les sous-traitants ;
- Variabilité de temps de mise en œuvre (compétence des équipes, climat…) …
On peut donc dire qu’il y a une part d’aléatoire dans les prix unitaires et quantités.
Chaque quantité ou prix unitaire est donc connu avec un delta près variable.
On admet que ce delta est une variable aléatoire qui suit une loi de probabilité.
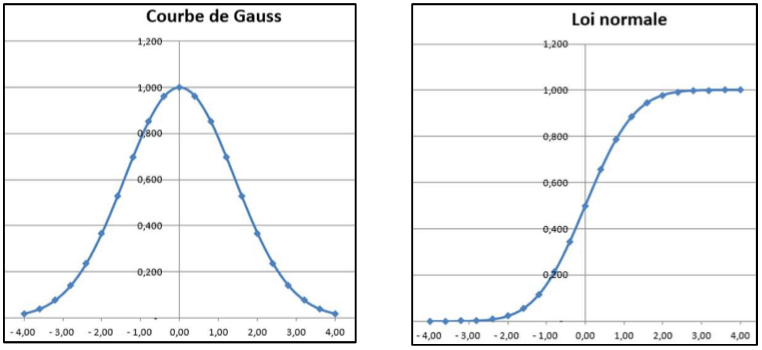
La loi de probabilité retenue est la loi normale centrée réduite N(0;1) , encore appelée loi « standard » (courbe de Gauss). Ce que l’on peut retenir c’est que plus on s’éloigne de la valeur moyenne, plus la probabilité chute rapidement (courbe en cloche).
Sa fonction de répartition s’écrit :
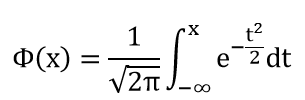
Remarque : la loi Normale, souvent notée N(µ ;σ²), est la « loi aimée des ingénieurs ». Sa densité a pour expression générale :

Avec σ : écart-type et µ : moyenne de distribution.
« Cette loi occupe une place privilégiée parmi toutes les lois de probabilités. Cela tient en particulier au théorème central limite. Celui-ci démontre, en effet, que la somme de n variables aléatoires suivant la même loi, converge en probabilité vers la loi Normale, indépendamment du type de fonction de répartition des variables, lorsqu’on fait croître n. Il n’est donc pas surprenant que, dans la nature, de nombreux phénomènes puissent sembler obéir à une loi Normale. »
Remarque : lorsque le prix unitaire est un prix composé de plusieurs variables aléatoires, par exemple n valeurs (comme en gros œuvre : main d’œuvre, matériel, matériaux…), on choisira comme loi de probabilité la loi Normale N(0;n). La dispersion des valeurs sera donc plus grande.
Chaque delta a une valeur minimale et maximale, par exemple +3% et -3% soit Δ- et Δ+. Pour simuler la variation de valeur, on peut calculer plusieurs scénarios en prenant une valeur de delta comprise entre Δ- et Δ+. Cette valeur suit la fonction de répartition de la loi « standard ».
Par calculs répétés, les différentes valeurs de quantités et de prix unitaires sont prises en compte et les différentes valeurs de prix total sont obtenus.

Par analyse de la courbe de répartition des prix totaux, le risque que le prix soit supérieur peut être déterminé. En connaissant le risque, un aléa peut être envisagé, et un nouveau prix total déterminé.
Exemple : revêtements de sols durs et murs durs
Examinons un exemple d’approche probabiliste du prix de la construction pour le lot sols et murs durs d’une étude de prix en bâtiment.
Prix total obtenu de façon déterministe, c’est-à-dire un calcul classique d’étude de prix avec une quantité fixée et un prix unitaire fixée : 775 340€.
Pour générer la courbe des valeurs que peut prendre ce lot, nous avons pris en compte les quantités avec +/- 5% et les prix unitaires avec +/- 10%.
Notre programme a produit 1024 valeurs équiprobables comprises entre 664 776€ et 893 244€. En d’autres termes, en prenant les écarts sur les quantités et les prix unitaires, on pourrait obtenir pour ce lot, un prix qui varie entre 664 776€ et 893 244€.
Bien sûr, on comprend rapidement que cet écart important peut dans un cas nous faire gagner une opération ou dans l’autre cas nous la faire perdre.
On comprend aussi mieux qu’une étude de prix n’est pas une science exacte.

La courbe en bleu se lit de la façon suivante, si en abscisse 825 000€ est retenu, 75% est obtenu en ordonnée ; cela signifie que 75% des valeurs générées sont inférieures à 825 000€. En d’autre terme, il y a 75% de chances que le prix réel du lot revêtement de sol soit inférieur à 825 000€.
La valeur déterministe est proche de la moyenne de l’ensembles des valeurs générées.
On peut tracer une nouvelle courbe des valeurs moyennes en fonction du % de valeurs retenues.
Par exemple pour 75%, on fait la moyenne des valeurs inférieures à 75%, c’est-à-dire la moyenne des valeurs entre 664 776€ et 825 000€.

La courbe en vert représente la moyenne des valeurs inférieures.
Imaginons que seulement 75% des valeurs soient retenues (les plus petites) et qu’on en fasse la moyenne (comme pour le calcul déterministe). On obtient un nouveau prix total sur la courbe verte à 752 000€ soit un rabais de 3% par rapport au déterministe.
On peut alors tracer la courbe du rabais par rapport au % de valeurs (les plus petites) retenu :

En fonction du risque que l’on veut prendre (% de valeurs retenu), on peut déterminer le rabais à appliquer.
L’approche probabiliste du prix de la construction montre bien que l’étude de prix n’est pas une science exacte. Les aléas sur les prix et les quantités explique notamment pourquoi des offres d’entreprises sur un même projet peuvent être très différentes.

